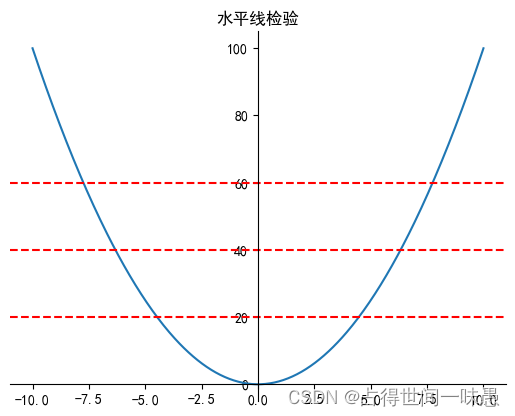
udp
散列表
sqoop
渲染
力扣
two sum
macos
数维杯
交友
WT-VL53L0 L1
mysql存储过程
NOIP
三栏布局
数据库增删改查
swing
EDraw Max
天气数据分析
AMQP
springboot二手交易
解压
微积分
2024/4/11 18:58:32数学分析:集合的基本运算
文章目录数学分析:集合的基本运算集合的并集合的交集合的差集合的补集合的运算律参考文献数学分析:集合的基本运算
集合有 并、交、差、补 四种基本运算。
集合的并
定义 1(集合的并):设 A,BA,BA,B 为两个集合&…
数学分析:数项级数的性质
数学分析:数项级数的性质
通过上一节的内容,我们知道:级数的收敛与数列的收敛本质上是一回事。这使得通过数列的性质推导级数的性质成为了可能。
定理 1. 数项级数收敛的必要条件:设 ∑n1∞xn\sum_{n1}^{\infty}x_{n}∑n1∞xn…
数列极限:数列极限的概念
文章目录数列极限的概念数列基础数列的概念特殊数列等差数列(算术数列)等比数列(几何数列)有界数列单调数列子列数列极限数列极限的定义数列极限的几何意义方式一方式二数列的敛散性分析参考文献数列极限的概念
这一节࿰…
微积分——用积分定义自然对数的动机
第6章 对数函数,指数函数和反三角函数 目录
第6章 对数函数,指数函数和反三角函数
6.1 引言
6.2 用积分定义自然对数的动机
内容来源:<> Tom M. Apostol 6.1 引言
每当有人将他的注意力集中到数量关系的时候,他要么是…
转动圈数累积功能块(数值积分器)
1、SMART PLC 流量累积功能块请参考下面文章链接:
https://rxxw-control.blog.csdn.net/article/details/134542089https://rxxw-control.blog.csdn.net/article/details/1345420892、博途PLC 流量累积功能块
https://rxxw-control.blog.csdn.net/article/details/126004031…
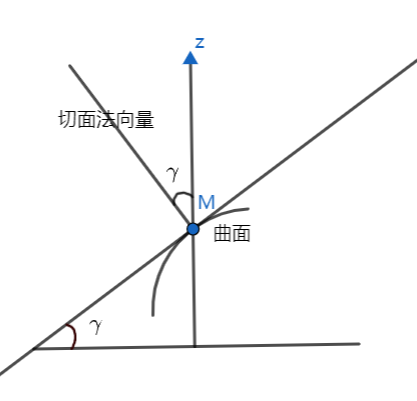
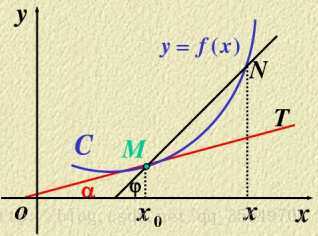
专题:曲面的切平面、法线
假设曲面方程为隐函数 F ( x , y , z ) 0 ,点 M ( x 0 , y 0 , z 0 ) 是其上一点 又在点 M 处任意引一条在曲面上的曲线,设该曲线参数方程为: { x φ ( t ) y ψ ( t ) z ω ( t ) ,且当 t t 0 时, x x 0 , y y…
微积分-第一章函数2
1.3 反函数
反函数顾名思义就是将原函数的输出逆反回原函数输入的函数。反函数的输入是原函数的输出,反函数的输出就是原函数的输入。函数 f f f的反函数,记作 f − 1 ( y ) f^{-1}(y) f−1(y)。
考虑函数 f ( x ) 5 x 2 f(x)5x2 f(x)5x2,想要求得在…
微积分 - 对数函数与指数函数的导数
指数法则 对数法则
换底法则:对于任意的底数b>1和c>1以及任意的数x>0有:
对数函数和指数函数求导
令,那么g的导数是什么?使用导数的定义我们得到: 我们如何来简化这个杂乱的公式呢?当然是使用对数法则了&a…
回顾【数学基础】找出断层,继续前进, 使用chatGPT学习并解决实际问题:微积分
已经学过的算术、代数、几何。跳过。
从微积分开始
想象一下,你在画一条曲线,或者在一个大草地上奔跑。微积分就是一种数学工具,帮助我们了解这条曲线的形状,或者你奔跑的方式。 微分(就像研究曲线上的每一小点&…
微积分-第二章三角函数(合集)
第二章三角函数
在处理微积分问题时,我们不可避免的会遇到三角函数。学会三角函数对于微积分是非常重要的。
2.1基本知识
学习三角函数我们需要先学习一些基本知识。 首先要学习的是弧度的概念。弧度是一种角的度量单位,用于测量角的大小。它是根据角…
数学分析:定积分的概念
数学分析笔记——总目录 文章目录定积分的概念定积分的产生背景定积分的定义参考文献定积分的概念
定积分的产生背景 \quad不定积分 与 定积分 是积分学中的两大基础问题,在不定积分部分,我们知道,不定积分是求导的逆运算,而本节…
【人工智能里的数学】多元函数的微分学
【人工智能里的数学】多元函数的微分学
系列文章目录
【人工智能学习笔记】人工智能里的数学——概述 【人工智能里的数学】一元函数微分学 【人工智能里的数学】线性代数基础 【人工智能里的数学】多元函数微分学
文章目录 文章目录 系列文章目录文章目录偏导数高阶偏导数梯…
[AGC032F]One Third
Description
一个长度为1的环,随机角度切n刀,对于每一块长度为x的,取最接近1/3的,即|x-1/3|最小的那一块 问这个最小值的期望 n<10^6
Solution
感觉还是有一些不明觉厉 首先,对于一次在x的划分,在x画…
高等数学上册 第十章 重积分 第十一章 曲线积分与曲面积分 知识点总结
重积分 二重积分计算法: 直角坐标下:化为二次积分 { 如果图形是 X Y 型,则都可以,但要考虑哪个计算不定积分方便 如果图形既不是 X 也不是 Y 型,则要拆分 极坐标下: ∬ f ( x , y ) d x d y ∬ f ( ρ cos…
微积分 - 洛必达法则的四种类型
洛必达法则
考虑如下形式的极限: 。因为f和g都是可导函数,所以可在xa点对他们进行线性化有: 和 。现在,假设f(a)和g(a)都为0,这说明和。如果f(x)除以g(x),假设则有
这就是洛必达法则。 类型A :
洛必达法则对于和的…
球面坐标系下的三重积分
涉及知识点
三重积分球面坐标系点火公式一些常见积分处理手法
球面坐标系定义
球面坐标系由方位角φ\varphiφ、仰角θ\thetaθ和距离rrr构成
直角坐标系(x,y,z)(x,y,z)(x,y,z)到球面坐标系的(r,φ,θ)(r,\varphi,\theta)(r,φ,θ)的转化规则如下: {xrsinφco…
微积分——Rolle定理的理解(罗尔定理)
极值定理(Extreme Value Theorem)指出,闭区间[a,b]上连续的函数既有最大值,也有最小值。然而,其最大最小值都可能发生在端点。罗尔定理(Rolle’s Theorem)以法国数学家Michel Rolle(1652-1719)的名字命名,它给出了极值存在于闭区间…
数学分析:函数的可积条件
文章目录函数的可积条件函数可积的必要条件函数可积的充要条件参考文献函数的可积条件
函数可积的必要条件 \quad在给出函数可积的充要条件之前,先来看函数可积的一个必要条件。
定理 1(可积的必要条件):若函数 f(x)f(x)f(x) 在…
数学分析:L‘Hospital 法则
数学分析笔记——总目录 文章目录LHospital 法则函数极限中的待定型处理 00\frac{0}{0}00 型的 LHospital 法则处理 ∗∞\frac{*}{\infty}∞∗ 型的LHospital 法则参考文献L’Hospital 法则
函数极限中的待定型 \quad接下来,我们只讨论如何使用 L’Hospital 法…
数学分析:Taylor多项式
数学分析笔记——总目录 文章目录Taylor 公式多项式函数的 Taylor 公式任意函数的Taylor公式带 Peano 余项的 Taylor 公式带Lagrange 余项的 Taylor 公式Maclaurin 公式参考文献Taylor 公式
多项式函数的 Taylor 公式 \quad设 p(x)p(x)p(x) 是 nnn 次整多项式: p(x…
常微分方程的解题思路
通解:独立常数的个数等于微分方程的阶数,独立常数的个数实际上就是 c 1 , c 2 , . . . , c n c_1,c_2,...,c_n c1,c2,...,cn是数目
所以补 C C C也是关键的一步,而且未必是 C C C,也可以是 ln C \ln C lnC之类的&…
微积分python基础
微积分基础(python) 文章目录 微积分基础(python)1 函数与极限2 求导与微分3 不定积分4 定积分 1 函数与极限
# 导入sympy库
from sympy import *
# 将x符号化
x Symbol("x")
xx \displaystyle x x
# 利用sympy中solve函数求解方程
X solve(x**2-10*x21,x)
X
pri…
函数极限的概念及性质
没看过数列极限的可以先看看: 数列极限的概念及性质 函数极限的概念函数定义函数的连续 函数的极限函数极限的描述性定义函数极限的定义函数极限的几何意义例题 函数极限的性质三个性质例题 四则运算法则关于无穷量小的比较例题 几个函数的等价替换 函数极限的概念…
前言【高等数学教程1(单变量微积分)】
前言【高等数学教程1(单变量微积分)】
1. 什么是高等数学?
目前大部分高等院校教授的高等数学(advanced mathematics)课程内容主要是微积分(calculus)。
1.1 微积分的发明
微积分有两位主要的发明人,牛顿和莱布尼茨。 牛顿除了…
数列极限的概念及性质
数列极限概念数列定义几何意义数列与函数 数列的极限实例数列极限的通俗定义数列极限的定义数列极限的几何定义 用极限定义证明极限的例题 收敛数列的性质四个法则运算法则例题 单调有界定理OStolz定理例题 公理Cauchy收敛准则例题 数列极限概念
数列
定义
如果按照某一法…
【用积分求抛物线与直线围成的面积】
文章目录 一、Problem Discription二、Sample Input and Sample Output三、数学分析与推导计算1. 根据抛物线顶点坐标 P 1 ( x 1 , y 1 ) P_1(x_1, y_1) P1(x1,y1)以及另一个点的坐标 P 2 ( x 2 , y 2 ) P_2(x_2, y_2) P2(x2,y2),求出抛物线方程2. 根据…
高等数学上册 第九章 多元函数微分法及其应用 知识点总结
多元函数微分法及其应用 ( 1 )多元函数的极限: 用“ ε − δ ”语言描述,二元函数的极限叫二重极限 二重极限存在: { 1 、 P ( x , y ) 一定要以任何方式趋于 ( x 0 , y 0 ) 时, f ( x , y ) 无限趋近于 A…
高数笔记03:几何、物理应用
图源:文心一言
本文是我学习高等数学几何、物理应用的一些笔记和心得,希望可以与考研路上的小伙伴一起努力上岸~~🥝🥝
第1版:查资料、画导图~🧩🧩
参考资料:《高等数学 基础篇》武…
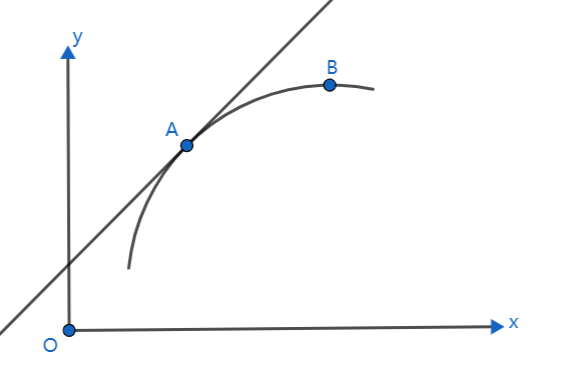
专题:平面、空间直线参数方程下的切线斜率问题
本文研究平面、空间直线在参数方程形式下,切线斜率(即导数)如何表示的问题。 如上图所示。 设 y f ( x ) , x φ ( t ) , y ψ ( t ) 当 t t 0 时, x x 0 , y y 0 ,即点 A 坐…
微积分-第一章函数(合集)
第一章函数
1.1 函数的定义
简单来说,函数就是一种规则,它将一个值作为输入映射到另一个值作为输出。如 f ( x ) 5 x f(x)5x f(x)5x。其中f称为函数, 5 x 5x 5x 是将输入 x x x映射到输出的规则, f ( x ) f(x) f(x)称为函数值或…
数学分析:数项级数的概念
数项级数的概念
一、引言
在正式进行数项级数的学习之前,先考虑这样一个问题:
公元前 450450450 年,古希腊有一位著名的学者芝诺(Zeno)曾提出了若干个影响数学史发展的悖论。考虑其中一个非常著名的悖论:…
数学分析:集合的基本概念
文章目录数学分析:集合的基本概念集合基础:定义集合基础:表示法枚举法枚举法——有限集合枚举法——无限集合描述法集合基础:性质集合基础:关系蕴含子集真子集相等参考文献数学分析:集合的基本概念
集合基…
数学分析:函数序列及其一致收敛性
文章目录函数序列及其一致收敛性函数序列函数序列的一致收敛性函数序列一致收敛性的判别法一致收敛的函数序列的性质参考文献函数序列及其一致收敛性 \quad此前,我们已经可以用收敛数列(或收敛的数项级数)来表示或定义一个数,接下…
数列极限:数列极限的性质
数学分析笔记——总目录 文章目录收敛数列的性质数列极限的唯一性收敛数列的有界性数列极限的保序性数列极限的夹逼性数列极限的运算性质——四则运算数列极限的和、差运算数列极限的乘运算数列极限的商运算参考文献收敛数列的性质 \quad这一节,介绍收敛数列的一些性…
定积分的几何应用(总结非常全面!)
文章目录 1 原函数存在性和可积性1.1 函数可积的充分条件(判定条件)1.2 函数存在原函数的充分条件(判定条件)1.3 函数可积的必要条件(性质)1.4 变上限积分的性质 2 平面图形2.1 平面图形的面积2.1.1 直角坐…
数学分析:换元积分法与分部积分法
8.2 换元积分法与分布积分法
一、换元积分法
定理 4:(第一类换元积分法) \quad设函数 f(x)f(x)f(x) 在区间 III 上有定义,φ(x)\varphi(x)φ(x) 在区间 JJJ 上可导,且 φ(J)⊂I\varphi(J) \subset Iφ(J)⊂I. 若不定…
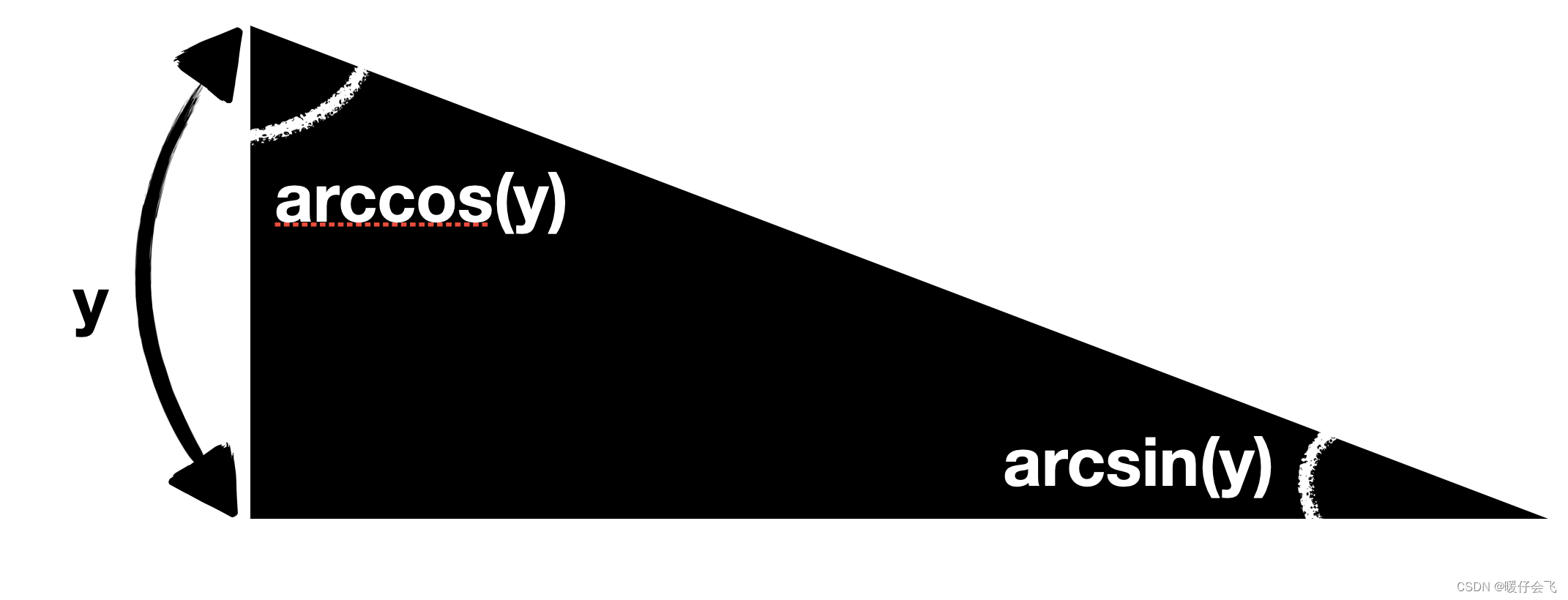
反函数求导:自然对数 ln是怎么得到的;为什么自然对数的导数是 1/ x;arcsin 和 arccos 的导数求算
参考视频:MIT微积分
如何得到的自然对数 lnlnln 首先我们知道以 eee 为底的指数函数 exe^xex 其次,我们引入反函数(逆函数)的概念 f−1(y)f^{-1}(y)f−1(y) 对于任意的 xxx 如果 f(x)yf(x)yf(x)y 那么 xf−1(x)xf^{-1}(x)xf−1(…
高等数学上册 第二章 导数与微分 知识点总结
导数与微分
与导数概念的形成有密切关系的两个历史问题:
直线运动的速度切线问题
导数概念:极限存在>可导,极限就是导数
导函数:某一区间内所有点都可导,其导数值构成的新的函数
单侧导数:可导的充…
一阶线性微分方程计算公式推导
一阶线性微分方程的形式如下: y′p(x)yq(x)yp(x)yq(x)y′p(x)yq(x) 对于式子左侧,长得像下式,但不太一样 (uv)′u′vuv′(uv)uvuv(uv)′u′vuv′ y′⋅1y⋅p(x)y 1y p(x)y′⋅1y⋅p(x) 这里对应vvv看似得不到一个合适的,但是借助[…